So far in our discussion of external ballistics, we’ve covered bullet trajectory, elevation, the Coriolis effect, light effects, rifle cant, and bullet shape, but we still have one more important ballistics theme to explore: static stability.
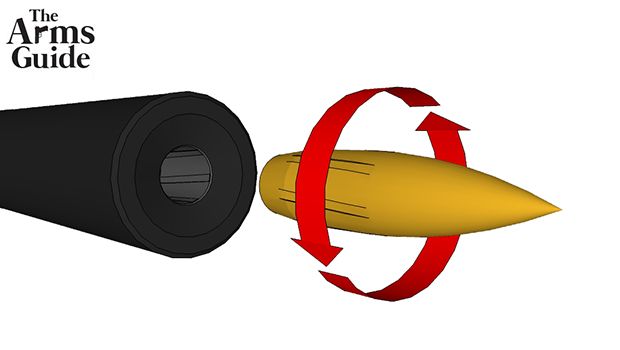
The concept of static stability is essential to precision rifle shooting; if bullets are not properly stabilized, you’ll never get consistent results at long distances, and sometimes not even with short range shots. In the previous article about bullet shape, I talked about why a bullet needs to be stabilized through spinning. Now we’ll discuss how the spinning, or gyroscopic motion, works to keep the bullet stabilized during its flight. Also, we’ll learn how to predict how a certain twist rate is capable of stabilizing a particular bullet.
The spinning motion, induced by the rifling of the barrel, keeps the bullet stable because of gyroscopic effect. This effect limits, or cancels, the destabilizing momentum. It is the same effect that you can observe playing with a spinning top that prevents the toy from falling on its side—due to gravity—while it’s spinning. The higher the destabilizing momentum, the highet the gyroscopic forces must be to keep the bullet stable. The gyroscopic force is a function of the spin rate: the higher the spin, the higher the gyroscopic stabilizing force. Thus, bullets with longer destabilizing momentum levers need higher spin rates.
The spin rate of the bullet depends on the barrel twist rate, and on the muzzle velocity. The twist rate is the number of twist that the barrel rifling does in a given space. On rifles specification it is usually indicated the distance that a rifling take to make a full twist, in example 1:10 indicate that the rifling make a full twist every ten inches. Obviously, the shorter the twist rate, the higher is the spin rate. Given a twist rate, the higher is the muzzle velocity, the higher is the spin rate.
When we chose an ammo for our rifle, or if we chose a rifle barrel for a specific ammunition, we must consider if the bullet will be stabilized by that specific twist rate at the specific muzzle velocity we predict we’ll obtain.
You may have heard or read that the appropriate twist rate is a function of the bullet weight, or vice versa, and that you must select the right bullet weight in consideration with your barrel’s the twist rate. That’s not completely true. As we have discussed before, it’s not the weight of the bullet that dictates the need for a shorter twist rate, it is the distance between the center of mass and the center of pressure. Although it’s true that heavier bullets are usually longer, it’s not necessarily true that lighter bullets always have a shorter destabilizing lever and will need longer twist rates. A heavy bullet with a long cylindrical part and a short nose will need less spin than a light bullet with a long tapered nose.
To see if a bullet can be stabilized or not by our rifle, we can use the Miller twist rule. I promised I would keep math out of this post, so I’ll give you two links of online calculators that will do all the math for you:
http://www.jbmballistics.com/cgi-bin/jbmstab-5.1.cgi
http://www.bergerbullets.com/litz/TwistRuleAlt.php
It is not specified on the JBM page, but, a bullet is generally considered stable if the stability factor (SG) is above 1.4.
Since the bullet length is required for the calculation, if you can’t physically measure your bullet, you can obtain the datum from here:
http://www.jbmballistics.com/ballistics/lengths/lengths.shtml
It’s important to understand that if a bullet is stable at the muzzle, it will remain stable for all the trajectory. This is because when travelling down range, the bullet speed drops faster than the spin rate. Thus, the destabilizing momentum of the air pushing on the center of pressure will decrease faster than the stabilizing gyroscopic force. Conversely, a bullet that’s unstable at the muzzle will not become stable down range, since the pitching and wobbling will keep it off the trajectory and the gyroscopic effect will only worsen the instability.
The spinning motion, and the consequent gyroscopic effect, is the cause of another series of issues that falls under the concept of dynamic stability. This will be the topic of the next article so, stay tuned!