We started off this long-range shooting series with an introduction to some important terminology. Now we’re ready to apply those terms.First, we will discuss what determines the vertical component of bullet trajectory. Then, in the next section, we’ll focus on what determines the horizontal component of the bullet trajectory.
Bullet Trajectory – Vertical Velocity
Let’s start with an introduction to a key external ballistics concept that directly relates to long-range shooting: bullet trajectory.
From the moment it leaves the muzzle, a bullet starts to follow a descending parabolic trajectory. This means that, as the bullet travels further, the rate at which it approaches the ground increases. This parabolic trajectory is caused by gravity and drag.
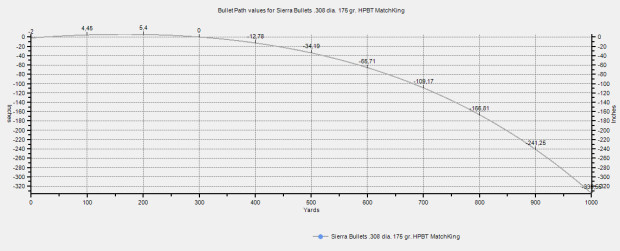
In fact, as soon as the bullet exits the barrel, it begins to fall toward the ground, attracted by gravity. The amount of drop caused by gravity is a function of bullet speed. Given a distance, the higher the bullet speed, the less is the time it is subjected to the effect of gravity and the less is its drop.
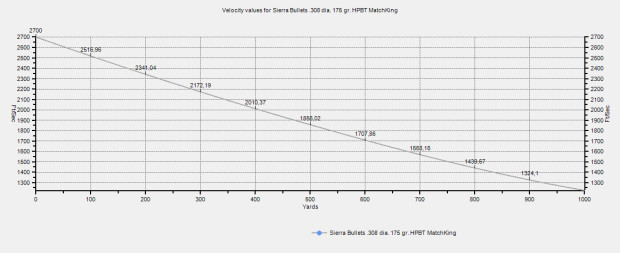
However, bullet speed is not constant; it starts to decrease as soon as the bullet exits the muzzle due to drag, the resistance that air offers to the bullet travel. As the speed decreases, the time the bullet is subjected to gravity increases, which, in turn, increases the amount of drop. This is what gives the bullet its parabolic trajectory.
How do you determine the amount of drag?
The amount of drag is determined by:
Bullet speed: Drag increases when the bullet speed, relative to the air, increases.
Ballistic coefficient: Bullets with higher BC are more efficient against drag.
Air density: The higher the air density, the higher is the drag. The density of the air depends essentially on:
Altitude/Atmospheric pressure: the higher the atmospheric pressure, the higher the air density.
Temperature: The lower the air temperature, the higher the air density.
Relative humidity: The higher the relative humidity, the higher the air density. Anyway, humidity has negligible effects on bullet drop, at least under 1000yds.
Wind: If the wind has a tail or head component, that is, if it does not blow perpendicular to the trajectory, it changes the speed of the air through which the bullet is flying. Therefore, the bullet speed relative to the air can change because of the wind changing the amount of drag on the bullet.
Wind can also affect the vertical component of the trajectory in a non-drag related manner. In fact, when a wind blows against a mountainside, a hillside, or a tall building, it generates a vertical component. A vertical wind can blow upward or downward, and the trajectory of a bullet that flies through it is deflected in that direction.
The Coriolis Effect
The Coriolis Effect is the effect of Coriolis force, that is, the force of the Earth’s rotation, on the bullet trajectory. Its effect is negligible, at least under about 1000yds, but we will examine this phenomenon in greater detail in the future.
Other factors must also be taken into account when dealing with the vertical component of the trajectory. These factors do not actually affect the trajectory but are aiming or prospective related errors. They are:
Firing elevation/depression angle: When shooting at an angle, in other words, shooting uphill or downhill, with a certain amount of line of sight angle relative to the horizon, the bullet always hits higher than the aimed point. This happens whether you are shooting uphill or downhill. The wider the firing angle, the higher the point of impact. It has a considerable effect on bullet impact, so it must be taken into account, even at short ranges, if the angle is more than 30°.
Light: The amount of light, and the direction from which it came, changes the way we see the target through a telescopic sight because of optical effects and distortions. This leads to point of aim and, consequently, point of impact changes.
I will talk about uphill/downhill shooting and light’s effect more thoroughly in the future.
Bullet Trajectory – Horizontal Velocity
In the section above, I talked about the variables that determine the vertical component of bullet trajectory (y-axis). In this section, we will examine what happens on the horizontal plane (x axis).
On the horizontal plane, the bullet does not follow a straight trajectory. From the moment it leaves the muzzle, it begins to be deflected by the effect of spindrift and, if present, wind.
Spindrift is the deflection caused by the gyroscopic motion of the bullet. This motion, aside from keeping the bullet stable and pointed forward, deflect it in the direction of the spin. If the barrel rifling has a right-handed (RH) twist, the bullet has a right-handed spin and is deflected toward right.
Vice versa, if it has a left-handed (LH) twist, the bullet is deflected toward left. The amount of drift is in the function of the spin rate relative to the bullet length. The higher the spin rate, the higher the drift. The spin rate depends on barrel twist rate and bullet speed. Shorter twist rates and higher bullet speeds produce higher spinning rates. In a future article we will examine the reason of the spin drift phenomenon.
Wind: The air in which the bullet flies behaves as a fluid. When it moves, under the effect of wind, the bullet traveling through it tends to move with it. To better understand this concept, think of the bullet as a raft crossing a river. It moves forward toward the other bank, but at the same time, it is pushed downriver by the stream. The result is that the raft does not reach the opposite bank at the point directly across from where it started, but instead lands further down-river. The bullet flying through a wind has the same behaviour.
The deflection caused by wind depends on several factors, including:
Wind speed: The higher the wind speed, the higher the deflection.
Time of flight: The shorter the time of flight, the shorter the time the bullet is pushed by the wind and, therefore, lower the deflection. Time of flight is dependent on bullet speed: the higher the bullet speed, the shorter the time of flight to a given distance.
Angle of incidence: A wind that blows perpendicular to the trajectory will have the most impact, while winds with different angles will have less influence. Winds that blow parallel to the trajectory, in other words head winds and tail winds, have no effect on the horizontal component of the trajectory.
Ballistic coefficient: Bullets with higher BC have better aerodynamics, so they are less affected by drag and their time of flight is shorter.
Bullet weight: Heavier bullets offer more resistance to the deflection. In addition, heavier bullets have often a higher BC.
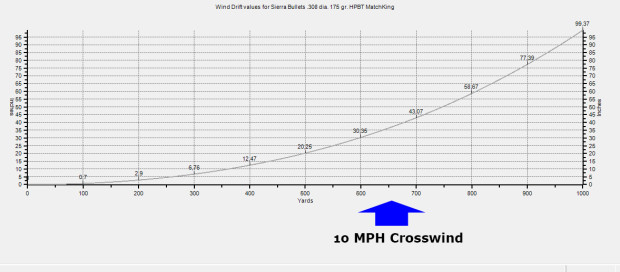
On the image above, you can see the effect of a 10mph wind, coming straight from the right, on a .308 Win long range bullet. As you can see, the deflection is not linear, but parabolic. Indeed, with the distance increasing and bullet slowing down, wind deflection increases more and more.
Coriolis Effect must be taken into account when compensating on the horizontal plane. The error due to Coriolis force is always toward the right on the northern hemisphere, and always toward the left on the southern hemisphere. It is in function of latitude and bullet speed. It is negligible until about 1000y.
Light, as with the vertical plane, has an effect on the horizontal path of trajectory. Light angle changes can lead to subtle, but yet detectable, changes in point of aim and consequently in point of impact.